Locally Linear Embedding

CodeSnippet

You can download all the code on this page from the code snippets directory

Locally linear embedding (LLE) approximates the input data with a low-dimensional surface and reduces its dimensionality by learning a mapping to the surface. Here we consider data generated randomly on an S-shaped 2D surface embedded in a 3D space:

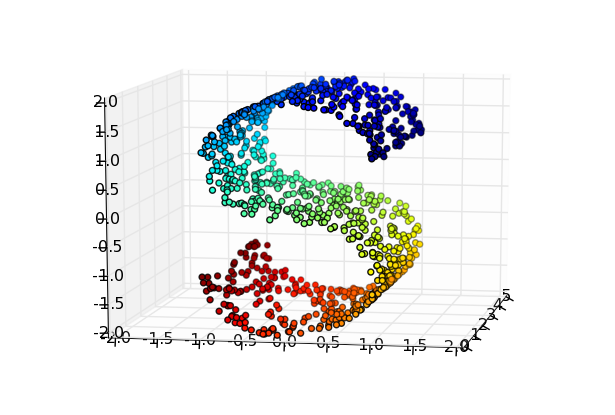
The surface is defined by the function

>>> def s_distr(npoints, hole=False):
...     """Return a 3D S-shaped surface. If hole is True, the surface has
...     a hole in the middle."""
...     t = mdp.numx_rand.random(npoints)
...     y = mdp.numx_rand.random(npoints)*5.
...     theta = 3.*mdp.numx.pi*(t-0.5)
...     x = mdp.numx.sin(theta)
...     z = mdp.numx.sign(theta)*(mdp.numx.cos(theta) - 1.)
...     if hole:
...         indices = mdp.numx.where(((0.3>t) | (0.7<t)) | ((1.>y) | (4.<y)))
...         return x[indices], y[indices], z[indices], t[indices]
...     else:
...         return x, y, z, t

We generate 1000 points on this surface, then define an LLENode with parameters k=15 (number of neighbors) and output_dim=2 (the number of dimensions of the reduced representation), then train and execute the node to obtain the projected data:

>>> n, k = 1000, 15
>>> x, y, z, t = s_distr(n, hole=False)
>>> data = mdp.numx.array([x,y,z]).T
>>> lle_projected_data = mdp.nodes.LLENode(k, output_dim=2)(data)

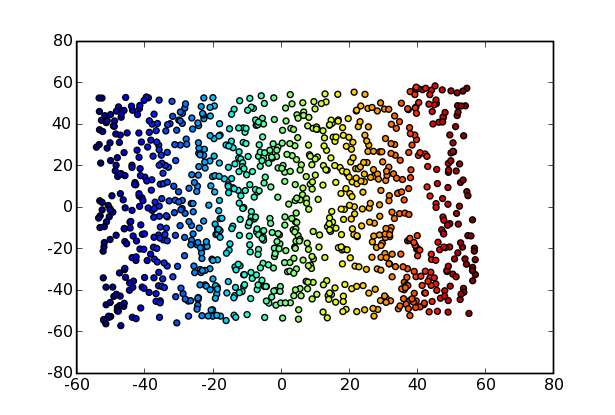
The projected data forms a nice parametric representation of the S-shaped surface:

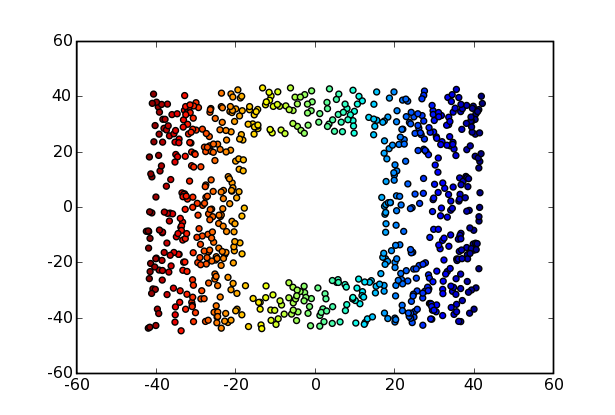
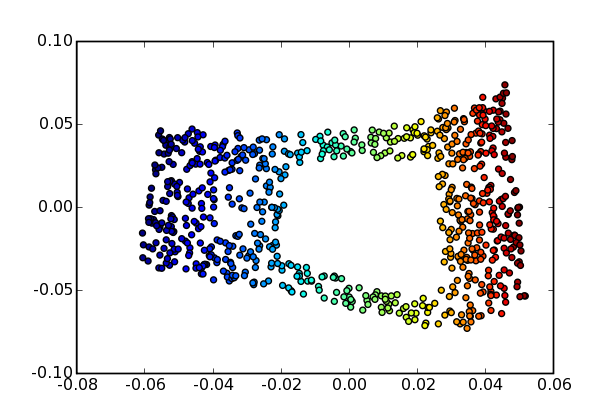
The problem becomes more difficult if the surface has a hole in the middle:

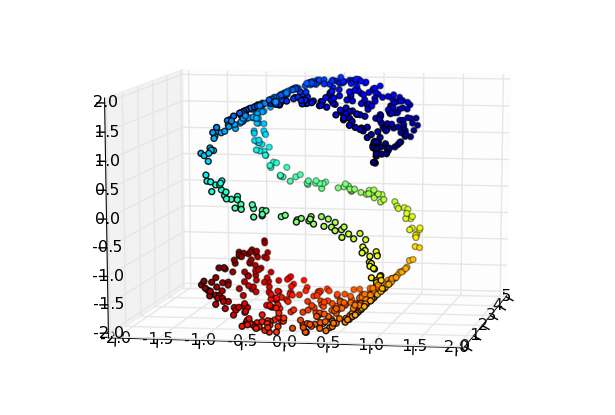
In this case, the LLE algorithm has some difficulty finding the correct representation. The lines

>>> x, y, z, t = s_distr(n, hole=True)
>>> data = mdp.numx.array([x,y,z]).T
>>> lle_projected_data = mdp.nodes.LLENode(k, output_dim=2)(data)

return a distorted mapping:

The Hessian LLE Node takes the local curvature of the surface into account, and is able to find a better representation:

>>> hlle_projected_data = mdp.nodes.HLLENode(k, output_dim=2)(data)